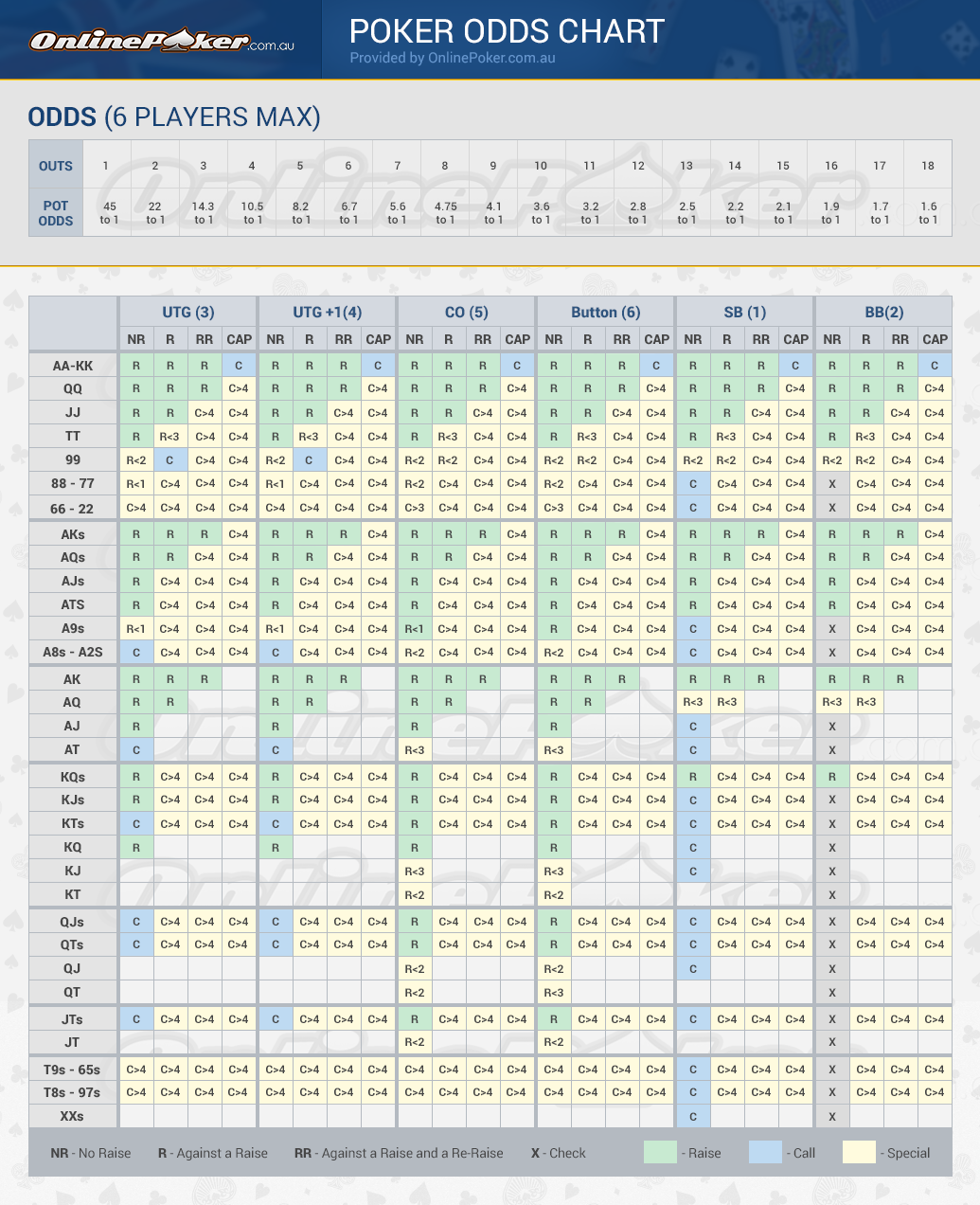
- Important Poker Probabilities Calculator
- Important Poker Probabilities Games
- Important Poker Probabilities Rules
- Important Poker Probabilities Cheat
- Important Poker Math
| Part of a series on |
| Strategy |
|---|
|
|
|
|
Poker Mathematics. Poker is a game of skill and using the ability to read situations and opponents to give you the advantage in each hand you play. It is also a game of mathematics, where you should be able to calculate the odds of either you or your opponent winning the hand in any situation. At low stakes online play, bluffing is much less important than a good understanding of the probabilities of winning hands. Big blinds won/100 hands The three stats I've presented so far mean nothing if you can't keep your win rate positive.
Poker is a popular card game that combines elements of chance and strategy. There are various styles of poker, all of which share an objective of presenting the least probable or highest-scoring hand. A poker hand is usually a configuration of five cards depending on the variant, either held entirely by a player or drawn partly from a number of shared, community cards. Players bet on their hands in a number of rounds as cards are drawn, employing various mathematical and intuitive strategies in an attempt to better opponents.
Given the game's many different forms and various dynamics, poker strategy becomes a complex subject. This article attempts to introduce only the basic strategy concepts.
The fundamental theorem of poker[edit]
The fundamental theorem of poker, introduced by David Sklansky, states: Every time you play your hand the way you would if you could see your opponents' cards, you gain, and every time your opponents play their cards differently from the way they would play them if they could see your cards, you gain.[1] This theorem is the foundation for many poker strategy topics. For example, bluffing and slow-playing (explained below) are examples of using deception to induce your opponents to play differently from how they would if they could see your cards. There are some exceptions to the fundamental theorem in certain multi-way pot situations, as described in Morton's theorem.
Pot odds, implied odds and poker probabilities[edit]
The relationship between pot odds and odds of winning is one of the most important concepts in poker strategy. Pot odds are the ratio of the size of the pot to the size of the bet required to stay in the pot.[1] For example, if a player must call $10 for a chance to win a $40 pot (not including their $10 call), their pot odds are 4-to-1. To have a positive expectation, a player's odds of winning must be better than their pot odds. If the player's odds of winning are also 4-to-1 (20% chance of winning), their expected return is to break even (on average, losing four times and winning once for every five times they play such a pot).
Implied odds is a more complicated concept, though related to pot odds. The implied odds on a hand are based not on the money currently in the pot, but on the expected size of the pot at the end of the hand. When facing an even money situation (like the one described in the previous paragraph) and holding a strong drawing hand (say a Four flush) a skilled player will consider calling a bet or even opening based on their implied odds. This is particularly true in multi-way pots, where it is likely that one or more opponents will call all the way to showdown.
Deception[edit]
By employing deception, a poker player hopes to induce their opponent(s) to act differently from how they would if they could see their cards. David Sklansky has argued that winning at poker is often decided by how much one player can force another to change his/her style while successfully maintaining their own strategy.[2]Bluffing is a form of deception where players bet strongly on a weak hand to induce opponents to fold superior hands. Related is the semi-bluff, in which a player who does not have a strong hand, but has a chance to improve it to a strong hand in later rounds, bets strongly on the hand in the hopes of inducing other players with weaker 'made' hands to fold. Slow-playing is deceptive play in poker that is roughly the opposite of bluffing: checking or betting weakly with a strong holding, attempting to induce other players with weaker hands to call or raise the bet instead of folding, to increase the payout.
Position[edit]
Position refers to the order in which players are seated around the table and the strategic consequences of this. Generally, players in earlier position (who have to act first) need stronger hands to bet/raise or call than players in later position. For example, if there are five opponents yet to act behind a player, there is a greater chance one of the yet to act opponents will have a better hand than if there were only one opponent yet to act. Being in late position is an advantage because a player gets to see how their opponents in earlier position act (which provides the player more information about their hands than they have about his). This information, coupled with a low bet to a late player, may allow the player to 'limp in' with a weaker hand when they would have folded the same hand if they'd had to act earlier. Position is one of the most vital elements to understand in order to be a long-term winning player. As a player's position improves, so too does the range of cards with which they can profitably enter a hand. Conversely this commonly held knowledge can be used to an intelligent poker player's advantage. If playing against observant opponents, then a raise with any two cards can 'steal the blinds,' if executed against passive players at the right time.
Reasons to raise[edit]
Unlike calling, raising has an extra way to win: opponents may fold. An opening bet may be considered a raise from a strategy perspective. David Sklansky gives seven reasons for raising, summarized below.[1]
- To get more money in the pot when a player has the best hand: If a player has the best hand, raising for value enables them to win a bigger pot.
- To drive out opponents when a player has the best hand: If a player has a made hand, raising may protect their hand by driving out opponents with drawing hands who may otherwise improve to a better hand.
- To bluff A player raises with an inferior or 'trash' hand attempts to deceive other players about the strength of their hand, and hopefully induce a better hand to fold.
- To semi-bluff A player with a drawing hand may raise both to bluff and for value. While technically still a bluff, as the player may not end up with a made hand and is primarily trying to drive out players, the player still has the opportunity to make his or her hand and win the pot if the bluff is called.
- To block Players on drawing hands may put out a 'blocking bet' against players who are likely to bet when checked to, but unlikely to raise when bet into. This is a small bet made on a drawing hand to lessen the likelihood of having to call a larger bet from a player in late position.
- To get a free card: If a player raises with a drawing hand, their opponent may call the bet and check to them on the next betting round, giving them a chance to get a free card to improve their hand.
- To gain information: If a player raises with an uncertain hand, they gain information about the strength of their opponent's hand if they are called. Players may use an opening bet on a later betting round (probe or continuation bets) to gain information by being called or raised (or may win the pot immediately).
- To drive out worse hands when a player's own hand may be second best: A combination protection and probe raise, a player with a strong hand but not the 'nuts' (the hole cards that make the best possible hand given the current face-up cards) may raise, both to induce drawing hands that may improve to the 'nut hand' to fold, while also testing to see if another player has the 'nuts'.
- To drive out better hands when a drawing hand bets: If an opponent with an apparent drawing hand has bet before the player to act, if the player raises, opponents behind them who may have a better hand may fold rather than call two bets 'cold'. This is a form of isolation play, and has elements of blocking and protection.
Reasons to call[edit]
There are several reasons for calling a bet or raise, summarized below.
- To see more cards: With a drawing hand, a player may be receiving the correct pot odds with the call to see more cards.
- To limit loss in equity: Calling may be appropriate when a player has adequate pot odds to call but will lose equity on additional money contributed to the pot with a raise.
- To avoid a re-raise: Only calling (and not raising) denies the original bettor the option of re-raising. However, this is only completely safe in case the player is last to act (i.e. 'closing the action').
- To conceal the strength of a player's hand: If a player has a very strong hand, they might smooth call on an early betting round to avoid giving away the strength of their hand on the hope of getting more money into the pot in later betting rounds.
- To manipulate pot odds: By calling (not raising), a player offers any opponents yet to act behind them more favorable pot odds to also call. For example, if a player has a very strong hand, a smooth call may encourage opponents behind them to overcall or even raise, building the pot. Particularly in limit games, building the pot in an earlier betting round may induce opponents to call future bets in later betting rounds because of the pot odds they will be receiving.
- To set up a bluff on a later betting round: Sometimes referred to as a long-ball bluff, calling on an earlier betting round can set up a bluff (or semi-bluff) on a later betting round. For instance, a player with a strong initial hand may call instead of raise to see the flop cheaply. That flop may not benefit the player, but the player may still have many 'outs' (cards left to deal that could make a strong hand), or even if the odds are slim they can try to bluff. By raising, this scenario may appear to an opponent like a player who has 'limped in' with a weak initial hand, but after the flop now has a strong made or drawing hand. A recent online term for 'long-ball bluffing' is floating.[3]
Gap concept[edit]
The gap concept states that a player needs a better hand to play against someone who has already opened (or raised) the betting than he would need to open himself.[4] The gap concept reflects that players prefer to avoid confrontations with other players who have already indicated strength, and that calling only has one way to win (by having the best hand), whereas opening may also win immediately if your opponent(s) fold.
Sandwich effect[edit]
Related to the gap effect, the sandwich effect states that a player needs a stronger hand to stay in a pot when there are opponents yet to act behind him.[3] Because the player does not know how many opponents will be involved in the pot or whether he will have to call a re-raise, he does not know what his effective pot odds actually are. Therefore, a stronger hand is desired as compensation for this uncertainty. A squeeze play exploits this principle.
Important Poker Probabilities Calculator
Loose/tight play[edit]
Loose players play relatively more hands and tend to continue with weaker hands; hence they do not often fold. Tight players play relatively fewer hands and tend not to continue with weaker hands; hence they often fold. The following concepts are applicable in loose games (and their inverse in tight games):[1]
- Bluffs and semi-bluffs are less effective because loose opponents are less likely to fold.
- Requirements for continuing with made hands may be lower because loose players may also be playing lower value hands.
- Drawing to incomplete hands, like flushes, tends to be more valuable as draws will often get favorable pot odds and a stronger hand (rather than merely one pair) is often required to win in multi-way pots.
Aggressive/passive play[edit]
Aggressive play refers to betting and raising. Passive play refers to checking and calling. Unless passive play is being used deceptively as mentioned above, aggressive play is generally considered stronger than passive play because of the bluff value of bets and raises and because it offers more opportunities for your opponents to make mistakes.[1]
Hand reading, tells and leveling[edit]
Important Poker Probabilities Games
Hand reading is the process of making educated guesses about the possible cards an opponent may hold, based on the sequence of actions in the pot. The term 'hand reading' is actually a misnomer, as skilled players do not attempt to assign a player to an exact hand. Rather they attempt to narrow the possibilities down to a range of probable hands based on the past actions of their opponent, during both the current hand and previous hands played by this opponent.
Tells are detectable changes in opponents' behavior or demeanor which provide clues about their hands or their intentions. Educated guesses about opponents' cards and intentions can help a player avoid mistakes in his own play, induce mistakes by the opponents, or influence the opponents to take actions that they would not normally take under the circumstances. For example, a tell might suggest that an opponent has missed a draw, so a player seeing it may decide a bluff would be more effective than usual.
Leveling or multiple level thinking is accounting for what the other opponents think about the hands. This information can then be used to the player's advantage. Some players might be able to make educated guesses about opponents' hands; this could be seen as the first level. The second level could be thought of as the combination of the first level and deducing what the opponents think the player's hand may be. Skilled players can adjust their game play to be on a higher level than that of less skilled opponents.
Table image and opponent profiling[edit]
By observing the tendencies and patterns of one's opponents, one can make more educated guesses about others' potential holdings. For example, if a player has been playing extremely tightly (playing very few hands), then when he/she finally enters a pot, one may surmise that he/she has stronger than average cards. One's table image is the perception by one's opponents of one's own pattern of play. A player can leverage their table image by playing out of character, and thereby inducing his/her opponents to misjudge his/her hand and make a mistake.
In live poker, as opposed to internet, stereotypes are often used for initial 'reads'. For instance, people of retirement age are often witnessed to play tight. Players will often project this image on unknown people of retirement age. Young people wearing headphones and hoodies are often witnessed to play more aggressively and mathematically if they played a lot of winning internet poker. These stereotypes can often be good bases to start a profile.
Often, there is a rather small pool of players in a given card playing venue. People will carry their history of playing with them in these environments.
Internet poker players can use large databases of hand histories to get a more precise player profile. Statistical information about opponents is displayed on the tables in the form of a heads up display. The most commonly used software is PokerTracker and Hold'em Manager.
Equity[edit]
Players' equity in a pot is their expected share of the pot, expressed either as a percentage (probability of winning) or expected value (amount of pot * probability of winning). Negative equity, or loss in equity, occurs when contributing to a pot with a probability of winning less than 1 / (number of opponents matching the contribution+1).
- Example
- Alice contributes $12 to a pot and is matched by two other opponents. Alice's $12 contribution 'bought' the chance to win $36. If Alice's probability of winning is 50%, her equity in the $36 pot is $18 (a gain in equity because her $12 is now 'worth' $18). If her probability of winning is only 10%, Alice loses equity because her $12 is now only 'worth' $3.60 (amount of pot * probability of winning).
- Texas hold 'em example
- Alice holds J♦8♠. Bob holds K♥7♠. After the flop, the board is 5♥6♥7♦. If both hands are played to a showdown, Alice has a 45% chance to win (which she is unaware of, because she does not know what hand Bob holds), Bob has a 53% chance to win and there is a 2% chance to split the pot. The pot currently has $51. Alice goes all-in for $45 reasoning that she can take the pot immediately if Bob folds or that Bob calls with a worse hand. Bob's simple pot odds for the call are also 32%; since his equity of 53% is greater than the pot odds he has to call, Bob has a positive expected value for the call (if he knew Alice's hole cards).
Short-handed considerations[edit]
When playing short-handed (at a table with 3-6 players), players must loosen up their play (play more hands) for several reasons:[1]
- There is less likelihood of another player having a strong hand because there are fewer players.
- Each player's share of the forced bets increases because there are fewer players contributing to the forced bets, thus waiting for premium hands becomes more expensive.
This type of situation comes up most often in tournament style play. In a cash game, the adjustments are very similar, but not quite as drastic as the table can ask for what is known as a 'rake break.' A rake break occurs when the floor-man, who represents the casino, agrees to take a smaller portion than usual for the hand. For example, a random casino might normally receive 10% of the pot up to 5 dollars for a 'rake.' In this case the table would only owe 10% up to 3 dollars until there are a sufficient number of players again. In online poker rake breaks are determined automatically.
Structure considerations[edit]
The blinds and antes and limit structure of the game have a significant influence on poker strategy. For example, it is easier to manipulate pot odds in no-limit and pot-limit games than in limit games. In tournaments, as the size of the forced bets relative to the chip stacks grows, pressure is placed on players to play pots to avoid being anted/blinded away.[5]
Mindset considerations[edit]
In 2014, Bwin conducted a study to see what makes a professional poker player. The brain activity of poker players, of varying degrees, was monitored using EEG headsets and visualised into brain maps.[6] Leading sports psychologist, James Hazlett, then interpreted the findings:
- More experienced players showed higher levels of focus and concentration throughout the game.
- The amateur players had less control over their emotions, and were prone to allowing negative emotions, such as frustration, distract them.
- Whilst opponents were taking their turn, the expert players opened up another table or watched replays of hands they had played poorly to improve.
- The brain maps showed that the professional players were led more by logic and intuition.
The conclusions of the study suggest that poker players can improve their strategy by considering their mindset. Mental training techniques, commonly used by athletes, could therefore help to improve performance by working on elements such as self-control and concentration.
See also[edit]
Poker plays[edit]
Specific games[edit]
Notes[edit]
- ^ abcdefDavid Sklansky (1987). The Theory of Poker. Two Plus Two Publications. ISBN1-880685-00-0.
- ^Milovsky, Nicholas. 'The Basics of Game Theory and Associated Games'. Retrieved 11 February 2014.
- ^ abDan Harrington and Bill Robertie (2004). Harrington on Hold'em: Expert Strategy For No-Limit Tournaments; Volume I: Strategic Play. Two Plus Two Publications. ISBN1-880685-33-7.
- ^David Sklansky (2001). Tournament Poker for Advanced Players. Two Plus Two Publications. ISBN1-880685-28-0.
- ^Dan Harrington and Bill Robertie (2005). Harrington on Hold'em: Expert Strategy For No-Limit Tournaments; Volume II: The Endgame. Two Plus Two Publications. ISBN1-880685-35-3.
- ^Your Brain on Poker
This post works with 5-card Poker hands drawn from a standard deck of 52 cards. The discussion is mostly mathematical, using the Poker hands to illustrate counting techniques and calculation of probabilities
Working with poker hands is an excellent way to illustrate the counting techniques covered previously in this blog – multiplication principle, permutation and combination (also covered here). There are 2,598,960 many possible 5-card Poker hands. Thus the probability of obtaining any one specific hand is 1 in 2,598,960 (roughly 1 in 2.6 million). The probability of obtaining a given type of hands (e.g. three of a kind) is the number of possible hands for that type over 2,598,960. Thus this is primarily a counting exercise.
___________________________________________________________________________
Preliminary Calculation
Usually the order in which the cards are dealt is not important (except in the case of stud poker). Thus the following three examples point to the same poker hand. The only difference is the order in which the cards are dealt.
These are the same hand. Order is not important.
The number of possible 5-card poker hands would then be the same as the number of 5-element subsets of 52 objects. The following is the total number of 5-card poker hands drawn from a standard deck of 52 cards.


The notation is called the binomial coefficient and is pronounced 'n choose r', which is identical to the number of -element subsets of a set with objects. Other notations for are , and . Many calculators have a function for . Of course the calculation can also be done by definition by first calculating factorials.
Thus the probability of obtaining a specific hand (say, 2, 6, 10, K, A, all diamond) would be 1 in 2,598,960. If 5 cards are randomly drawn, what is the probability of getting a 5-card hand consisting of all diamond cards? It is
This is definitely a very rare event (less than 0.05% chance of happening). The numerator 1,287 is the number of hands consisting of all diamond cards, which is obtained by the following calculation.
The reasoning for the above calculation is that to draw a 5-card hand consisting of all diamond, we are drawing 5 cards from the 13 diamond cards and drawing zero cards from the other 39 cards. Since (there is only one way to draw nothing), is the number of hands with all diamonds.
If 5 cards are randomly drawn, what is the probability of getting a 5-card hand consisting of cards in one suit? The probability of getting all 5 cards in another suit (say heart) would also be 1287/2598960. So we have the following derivation.
Thus getting a hand with all cards in one suit is 4 times more likely than getting one with all diamond, but is still a rare event (with about a 0.2% chance of happening). Some of the higher ranked poker hands are in one suit but with additional strict requirements. They will be further discussed below.
Another example. What is the probability of obtaining a hand that has 3 diamonds and 2 hearts? The answer is 22308/2598960 = 0.008583433. The number of '3 diamond, 2 heart' hands is calculated as follows:
Genting casino derby poker. One theme that emerges is that the multiplication principle is behind the numerator of a poker hand probability. For example, we can think of the process to get a 5-card hand with 3 diamonds and 2 hearts in three steps. The first is to draw 3 cards from the 13 diamond cards, the second is to draw 2 cards from the 13 heart cards, and the third is to draw zero from the remaining 26 cards. The third step can be omitted since the number of ways of choosing zero is 1. In any case, the number of possible ways to carry out that 2-step (or 3-step) process is to multiply all the possibilities together.
___________________________________________________________________________
The Poker Hands
Here's a ranking chart of the Poker hands.
The chart lists the rankings with an example for each ranking. The examples are a good reminder of the definitions. The highest ranking of them all is the royal flush, which consists of 5 consecutive cards in one suit with the highest card being Ace. There is only one such hand in each suit. Thus the chance for getting a royal flush is 4 in 2,598,960.
Royal flush is a specific example of a straight flush, which consists of 5 consecutive cards in one suit. There are 10 such hands in one suit. So there are 40 hands for straight flush in total. A flush is a hand with 5 cards in the same suit but not in consecutive order (or not in sequence). Thus the requirement for flush is considerably more relaxed than a straight flush. A straight is like a straight flush in that the 5 cards are in sequence but the 5 cards in a straight are not of the same suit. For a more in depth discussion on Poker hands, see the Wikipedia entry on Poker hands.
The counting for some of these hands is done in the next section. The definition of the hands can be inferred from the above chart. For the sake of completeness, the following table lists out the definition.

Definitions of Poker Hands
| Poker Hand | Definition | |
|---|---|---|
| 1 | Royal Flush | A, K, Q, J, 10, all in the same suit |
| 2 | Straight Flush | Five consecutive cards, |
| all in the same suit | ||
| 3 | Four of a Kind | Four cards of the same rank, |
| one card of another rank | ||
| 4 | Full House | Three of a kind with a pair |
| 5 | Flush | Five cards of the same suit, |
| not in consecutive order | ||
| 6 | Straight | Five consecutive cards, |
| not of the same suit | ||
| 7 | Three of a Kind | Three cards of the same rank, |
| 2 cards of two other ranks | ||
| 8 | Two Pair | Two cards of the same rank, |
| two cards of another rank, | ||
| one card of a third rank | ||
| 9 | One Pair | Three cards of the same rank, |
| 3 cards of three other ranks | ||
| 10 | High Card | If no one has any of the above hands, |
| the player with the highest card wins |
___________________________________________________________________________
Counting Poker Hands
Straight Flush
Counting from A-K-Q-J-10, K-Q-J-10-9, Q-J-10-9-8, …, 6-5-4-3-2 to 5-4-3-2-A, there are 10 hands that are in sequence in a given suit. So there are 40 straight flush hands all together.
Four of a Kind
There is only one way to have a four of a kind for a given rank. The fifth card can be any one of the remaining 48 cards. Thus there are 48 possibilities of a four of a kind in one rank. Thus there are 13 x 48 = 624 many four of a kind in total.
Full House
Let's fix two ranks, say 2 and 8. How many ways can we have three of 2 and two of 8? We are choosing 3 cards out of the four 2's and choosing 2 cards out of the four 8's. That would be = 4 x 6 = 24. But the two ranks can be other ranks too. How many ways can we pick two ranks out of 13? That would be 13 x 12 = 156. So the total number of possibilities for Full House is
Note that the multiplication principle is at work here. When we pick two ranks, the number of ways is 13 x 12 = 156. Why did we not use = 78?
Flush
There are = 1,287 possible hands with all cards in the same suit. Recall that there are only 10 straight flush on a given suit. Thus of all the 5-card hands with all cards in a given suit, there are 1,287-10 = 1,277 hands that are not straight flush. Thus the total number of flush hands is 4 x 1277 = 5,108.
Straight
There are 10 five-consecutive sequences in 13 cards (as shown in the explanation for straight flush in this section). In each such sequence, there are 4 choices for each card (one for each suit). Thus the number of 5-card hands with 5 cards in sequence is . Then we need to subtract the number of straight flushes (40) from this number. Thus the number of straight is 10240 – 10 = 10,200.
Three of a Kind
There are 13 ranks (from A, K, …, to 2). We choose one of them to have 3 cards in that rank and two other ranks to have one card in each of those ranks. The following derivation reflects all the choosing in this process.

The notation is called the binomial coefficient and is pronounced 'n choose r', which is identical to the number of -element subsets of a set with objects. Other notations for are , and . Many calculators have a function for . Of course the calculation can also be done by definition by first calculating factorials.
Thus the probability of obtaining a specific hand (say, 2, 6, 10, K, A, all diamond) would be 1 in 2,598,960. If 5 cards are randomly drawn, what is the probability of getting a 5-card hand consisting of all diamond cards? It is
This is definitely a very rare event (less than 0.05% chance of happening). The numerator 1,287 is the number of hands consisting of all diamond cards, which is obtained by the following calculation.
The reasoning for the above calculation is that to draw a 5-card hand consisting of all diamond, we are drawing 5 cards from the 13 diamond cards and drawing zero cards from the other 39 cards. Since (there is only one way to draw nothing), is the number of hands with all diamonds.
If 5 cards are randomly drawn, what is the probability of getting a 5-card hand consisting of cards in one suit? The probability of getting all 5 cards in another suit (say heart) would also be 1287/2598960. So we have the following derivation.
Thus getting a hand with all cards in one suit is 4 times more likely than getting one with all diamond, but is still a rare event (with about a 0.2% chance of happening). Some of the higher ranked poker hands are in one suit but with additional strict requirements. They will be further discussed below.
Another example. What is the probability of obtaining a hand that has 3 diamonds and 2 hearts? The answer is 22308/2598960 = 0.008583433. The number of '3 diamond, 2 heart' hands is calculated as follows:
Genting casino derby poker. One theme that emerges is that the multiplication principle is behind the numerator of a poker hand probability. For example, we can think of the process to get a 5-card hand with 3 diamonds and 2 hearts in three steps. The first is to draw 3 cards from the 13 diamond cards, the second is to draw 2 cards from the 13 heart cards, and the third is to draw zero from the remaining 26 cards. The third step can be omitted since the number of ways of choosing zero is 1. In any case, the number of possible ways to carry out that 2-step (or 3-step) process is to multiply all the possibilities together.
___________________________________________________________________________
The Poker Hands
Here's a ranking chart of the Poker hands.
The chart lists the rankings with an example for each ranking. The examples are a good reminder of the definitions. The highest ranking of them all is the royal flush, which consists of 5 consecutive cards in one suit with the highest card being Ace. There is only one such hand in each suit. Thus the chance for getting a royal flush is 4 in 2,598,960.
Royal flush is a specific example of a straight flush, which consists of 5 consecutive cards in one suit. There are 10 such hands in one suit. So there are 40 hands for straight flush in total. A flush is a hand with 5 cards in the same suit but not in consecutive order (or not in sequence). Thus the requirement for flush is considerably more relaxed than a straight flush. A straight is like a straight flush in that the 5 cards are in sequence but the 5 cards in a straight are not of the same suit. For a more in depth discussion on Poker hands, see the Wikipedia entry on Poker hands.
The counting for some of these hands is done in the next section. The definition of the hands can be inferred from the above chart. For the sake of completeness, the following table lists out the definition.
Definitions of Poker Hands
| Poker Hand | Definition | |
|---|---|---|
| 1 | Royal Flush | A, K, Q, J, 10, all in the same suit |
| 2 | Straight Flush | Five consecutive cards, |
| all in the same suit | ||
| 3 | Four of a Kind | Four cards of the same rank, |
| one card of another rank | ||
| 4 | Full House | Three of a kind with a pair |
| 5 | Flush | Five cards of the same suit, |
| not in consecutive order | ||
| 6 | Straight | Five consecutive cards, |
| not of the same suit | ||
| 7 | Three of a Kind | Three cards of the same rank, |
| 2 cards of two other ranks | ||
| 8 | Two Pair | Two cards of the same rank, |
| two cards of another rank, | ||
| one card of a third rank | ||
| 9 | One Pair | Three cards of the same rank, |
| 3 cards of three other ranks | ||
| 10 | High Card | If no one has any of the above hands, |
| the player with the highest card wins |
___________________________________________________________________________
Counting Poker Hands
Straight Flush
Counting from A-K-Q-J-10, K-Q-J-10-9, Q-J-10-9-8, …, 6-5-4-3-2 to 5-4-3-2-A, there are 10 hands that are in sequence in a given suit. So there are 40 straight flush hands all together.
Four of a Kind
There is only one way to have a four of a kind for a given rank. The fifth card can be any one of the remaining 48 cards. Thus there are 48 possibilities of a four of a kind in one rank. Thus there are 13 x 48 = 624 many four of a kind in total.
Full House
Let's fix two ranks, say 2 and 8. How many ways can we have three of 2 and two of 8? We are choosing 3 cards out of the four 2's and choosing 2 cards out of the four 8's. That would be = 4 x 6 = 24. But the two ranks can be other ranks too. How many ways can we pick two ranks out of 13? That would be 13 x 12 = 156. So the total number of possibilities for Full House is
Note that the multiplication principle is at work here. When we pick two ranks, the number of ways is 13 x 12 = 156. Why did we not use = 78?
Flush
There are = 1,287 possible hands with all cards in the same suit. Recall that there are only 10 straight flush on a given suit. Thus of all the 5-card hands with all cards in a given suit, there are 1,287-10 = 1,277 hands that are not straight flush. Thus the total number of flush hands is 4 x 1277 = 5,108.
Straight
There are 10 five-consecutive sequences in 13 cards (as shown in the explanation for straight flush in this section). In each such sequence, there are 4 choices for each card (one for each suit). Thus the number of 5-card hands with 5 cards in sequence is . Then we need to subtract the number of straight flushes (40) from this number. Thus the number of straight is 10240 – 10 = 10,200.
Three of a Kind
There are 13 ranks (from A, K, …, to 2). We choose one of them to have 3 cards in that rank and two other ranks to have one card in each of those ranks. The following derivation reflects all the choosing in this process.
Two Pair and One Pair
These two are left as exercises.
Important Poker Probabilities Rules
High Card
The count is the complement that makes up 2,598,960.
Important Poker Probabilities Cheat
The following table gives the counts of all the poker hands. The probability is the fraction of the 2,598,960 hands that meet the requirement of the type of hands in question. Note that royal flush is not listed. This is because it is included in the count for straight flush. Royal flush is omitted so that he counts add up to 2,598,960.
Probabilities of Poker Hands
| Poker Hand | Count | Probability | |
|---|---|---|---|
| 2 | Straight Flush | 40 | 0.0000154 |
| 3 | Four of a Kind | 624 | 0.0002401 |
| 4 | Full House | 3,744 | 0.0014406 |
| 5 | Flush | 5,108 | 0.0019654 |
| 6 | Straight | 10,200 | 0.0039246 |
| 7 | Three of a Kind | 54,912 | 0.0211285 |
| 8 | Two Pair | 123,552 | 0.0475390 |
| 9 | One Pair | 1,098,240 | 0.4225690 |
| 10 | High Card | 1,302,540 | 0.5011774 |
| Total | 2,598,960 | 1.0000000 |
Important Poker Math
___________________________________________________________________________
2017 – Dan Ma